Як зрозуміти топологію у 3D-моделюванні
Розуміння топології в 3D-моделюванні включає аналіз розподілу граней в моделі. Можливо, ви ставили собі такі запитання:
- Як визначити правильність розподілу ребер у моїй моделі?
- Чи можна сказати, що ребра рівномірно розподілені в сітці моделі?
- Як дізнатися, наскільки чиста моя сітка?
- Чи є проблеми із защемленням у моїй моделі?
- Чому після підрозділу сітка виглядає деформованою?
Відповісти на ці питання допоможе розуміння основ топології у 3D-моделюванні. Однак, немає універсальних правил або процесів, які можна застосувати до всіх проектів. Незважаючи на це, є прості правила, які потрібно запам'ятати. Однак, для вміння застосовувати ці правила до різних сіток потрібна практика та досвід.
З чого почати?
Отже, почнемо з визначенням того, що таке правильна топологія в 3D-моделюванні.
Дозвольте мені спочатку продемонструвати кілька прикладів, коли топологія стає проблематичною, а потім ми розглянемо можливе просте вирішення цієї проблеми.
У наступному прикладі ми можемо бачити, що у сітки виникають деякі проблеми через неправильну топологію. Однією з проблем є спотворення області, викликаного близьким розташуванням країв.
Тепер давайте подивимося, чи зможемо ми знайти просте вирішення цієї проблеми.
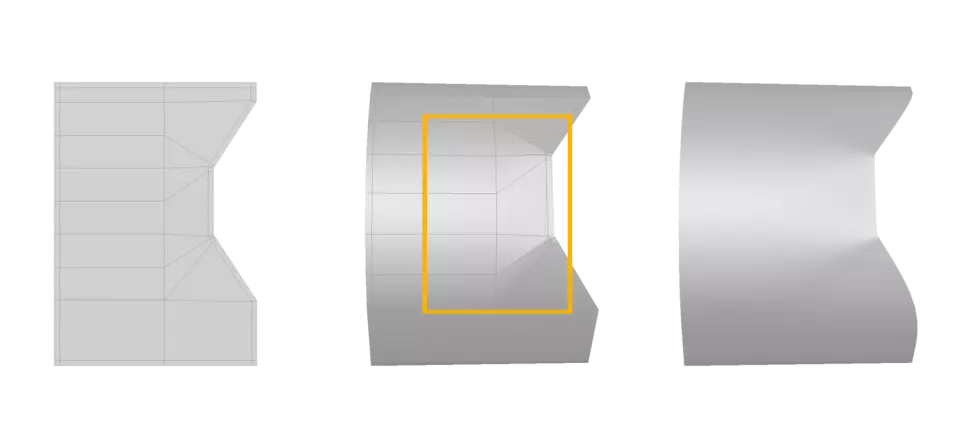
У цьому прикладі спостерігається спотворення в сітці моделі. Гострота області залежить від відстані між її ребрами - чим ближче ребра, тим різкіший кут вони утворюють. Однак, якщо на одному кінці ребра розташовані дуже близько, а на іншому - значно рознесені, може статися деформація.
На прикладі видно, що область з широким розкидом ребер поступово переходить в область з вузьким розкидом ребер. Перехід між цими областями викликає деформацію через недостатню геометрію для підтримки такої структури.
Простим вирішенням цієї проблеми є створення більш рівномірного розподілу граней (або ребер) у моделі. Додавання нових граней слід виконувати таким чином, щоб розподіл граней був рівномірним і був схожий на квадрати або ромби. Це допоможе зняти напругу та запобігти деформації.
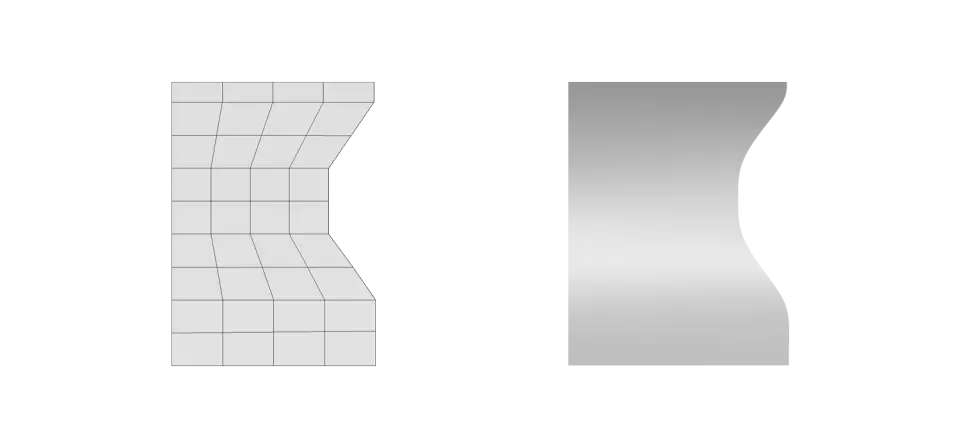
Правильна топологія вимагає не тільки рівномірного розподілу граней, але й достатньої кількості полігонів, щоб забезпечити деталізацію моделі.
Занадто низька кількість полігонів може призвести до спотворень зі збільшенням деталей. Однак не слід перевантажувати модель надмірною кількістю полігонів, оскільки це також може спричинити проблеми.
Робота з гранями має свої плюси та мінуси як при низькій, так і при високій щільності полігонів. Давайте розглянемо їхні переваги та недоліки.
Низька кількість полігонів (Low poly count)
➕ Низька кількість полігонів дозволить нам легко змінювати форму та блокувати ідею.
⛔ При низькій кількості полігонів ми не зможемо створити деталі. Чим більше деталей ми хочемо, тим більше геометрії нам знадобиться.Велика кількість полігонів (High poly count)
➕ При великій кількості полігонів ми легко можемо додати більше деталей і легко ущільнити сітку.
⛔ З іншого боку, сітки з великою кількістю полігонів складніше контролювати, так як у них більше точок та граней, якими потрібно маніпулювати.
Правила, які ми дотримуємося й досі
Отже, якщо ми узагальним цю інформацію, який висновок чи правило ми застосуємо до нашого робочого процесу?
1. Ми маємо починати з дуже низького полігонажу.
Чому? Тому що сіткою легше керувати, і вона допомагає нам швидше створити форму.
2. Ми повинні переконатися, що межі розподілені рівномірно.
Чому? Тому що ми хочемо бути впевнені, що у нас достатньо геометрії для наших деталей та гострих кутів. Нерівномірний розподіл граней може призвести до небажаних результатів, як ми бачили в першому прикладі.
Чудово! Два простих правила для початку. Не так вже й складно запам'ятати, вірно?
Але хіба це все?
Ні... у нас є ще два. Якщо ми зараз перевіримо наш прогрес, яким буде наш наступний крок?
Наш останній приклад показує, що геометрія не має спотворень завдяки рівномірно розподіленим граням, але тепер кути більше не гострі.
Щоб зробити це правильно, нам потрібно познайомитися з підтримуючими ребрами та потоком ребер. Давайте розглянемо це далі.
Підтримуючі ребра (Supportive Edges)
Що таке ребра, що підтримують?
Ребра, що підтримують, просто забезпечують збереження різкості об'єкта після застосування підрозділу.
Будь-яка грань/фігура, яку ми хочемо підтягнути, потребує як мінімум однієї або двох (рекомендується) підтримуючих ребер. Зазвичай це контур нашої моделі. Два краї, розташовані близько один до одного, утворюють гострий кут. Нам просто потрібно дотримуватися цього правила.
Отже, у нашому прикладі, де ми розташуємо опорне ребро? Ми вже згадували про контур, вірно?
У цьому випадку ми можемо або видавити краї контуру (показані жовтим кольором) назовні, або продублювати край з внутрішньої сторони. Таким чином, ми встановлюємо підтримуюче ребро.
Після екструдування фігури контурний край в ідеалі повинен бути оточений двома підтримуючими ребрами.
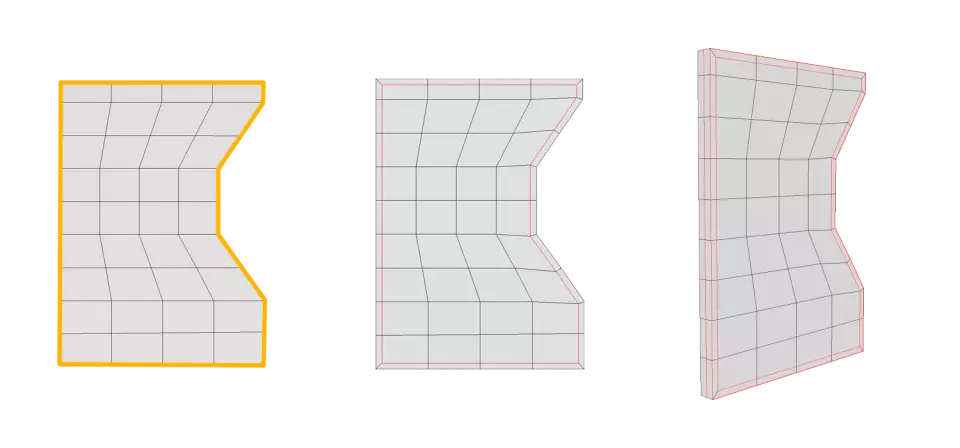
Тепер ми можемо швидко перевірити, як виглядатиме наша сітка із застосованим підрозділом. Все виглядає нормально, і здається, що на поверхні немає спотворень при згинанні. Поки що це досить добре.
Давайте додамо до нашого списку правил і ребра підтримки.
Правила, які ми дотримуємося досі
1. Ми повинні розпочинати дуже низьку кількість полігонів.
Чому? Тому що сіткою легше керувати і вона допомагає нам швидше створити форму.2. Ми повинні переконатися, що ребра рівномірно розподілені.
Чому? Тому що ми хочемо бути впевнені, що у нас достатньо геометрії для наших деталей та гострих кутів. Нерівномірний розподіл ребер може призвести до небажаних результатів, як ми бачили в першому прикладі.3. Нам потрібно додати ребра, що підтримують.
Чому? Тому що підтримуючі ребра забезпечать збереження структури нашої основної фігури (або контуру), коли ми застосуємо підрозділ.
Edge flow (потік ребер)
Що таке потік ребер і що таке перенаправлення ребер?
У багатьох ситуаціях перші три кроки не завжди дають бажаний результат. Деякі кути можуть бути не такими гострими чи м'якими, як ми хочемо.
У нашому випадку всі кути, як і раніше, дуже м'які, а не гострі та чіткі.
Тепер нам потрібен спосіб маніпулювати топологією, яка у нас вже є, щоб отримати бажаний результат, чи не так? Але не тільки це, нам також слід зберегти чистоту топології, зберігаючи при цьому квадрати.
Якщо ця область здається трохи заплутаною, просто потрібно попрактикуватися. Більше прикладів, через які ви пройдете, стануть зрозумілішими.
Давайте спочатку поговоримо про перенаправлення. Ми можемо почати з підтримуючих ребер, оскільки вони забезпечують достатню геометрію для формування гострого кута.
Якщо ми повернемося до самих основ, у нас буде два приклади. Один приклад матиме м'який кут, а інший – гостріший. Помітили різницю?
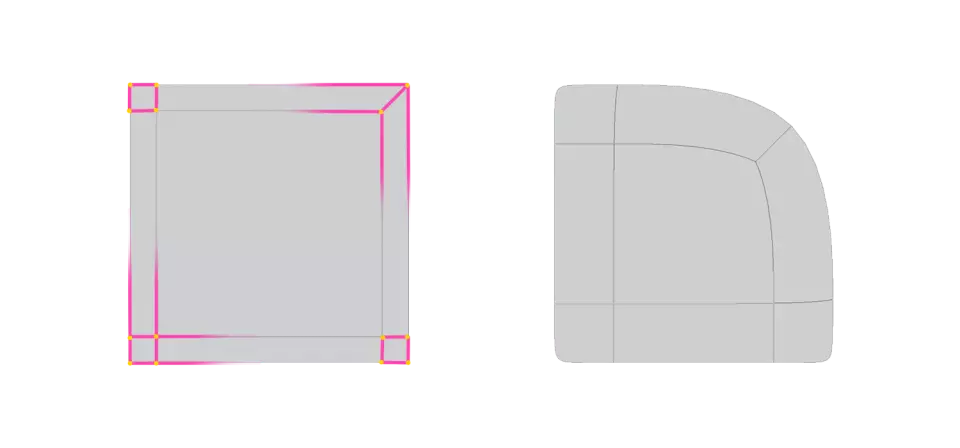
Отже, ґрунтуючись на наведеному вище прикладі, давайте продовжимо та застосуємо гострі кути, використовуючи підтримуючі ребра там, де це можливо.
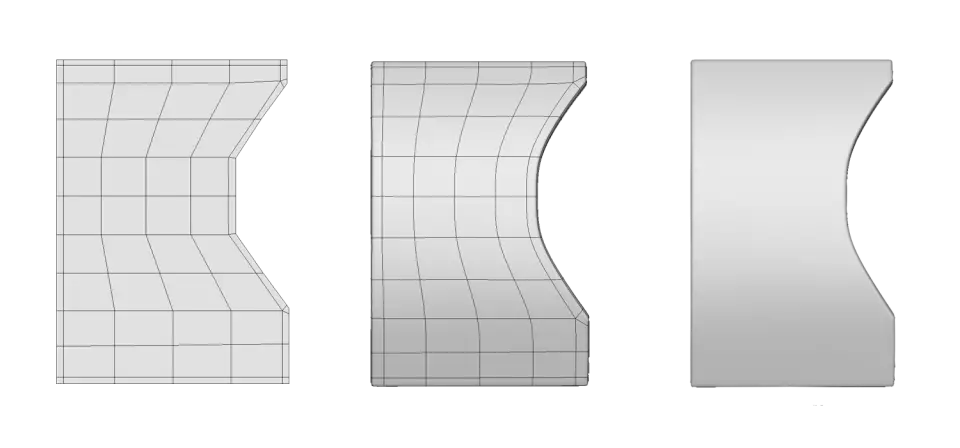
Тепер ми повільно наближаємося до остаточної форми, і, як ви можете помітити, залишилося заточити лише два кути.
Ось що ми збираємося зробити. Нам потрібно переставити наші ребра таким чином, щоб вони мали "гравітаційний потік". Скажіть, що?
Так, ця штука допомогла мені краще зрозуміти цю штуку з ребрами, так що, сподіваюся, вона допоможе і комусь іншому.
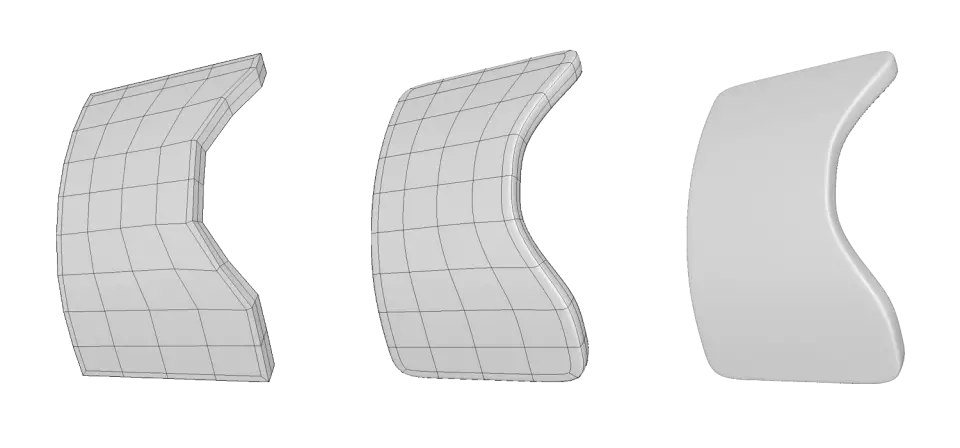
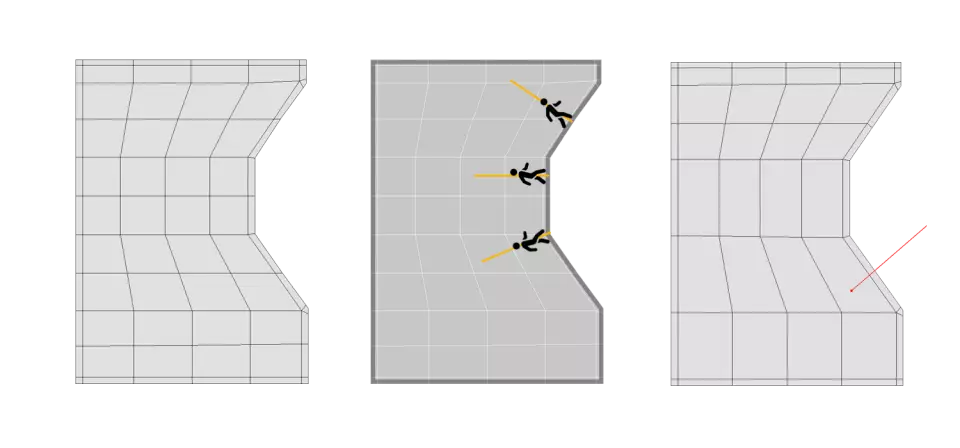
У прикладі нижче ми бачимо наш поточний потік граней зліва. Але тепер перевіримо приклад у середині.
У нас є сірий контур, який представляє наше підтримуюче ребро. Тепер давайте уявимо, що там є сила гравітації, і залежно від того, під яким кутом ми йтитемо, це буде потік для грані (показано жовтим). Нам просто потрібно застосувати цю логіку для перестановки граней, щоб вони працювали на користь форми.
У прикладі праворуч я прибрав непотрібні нам ребра, щоб у нас було більше місця для проходження "гравітації" нашої форми.
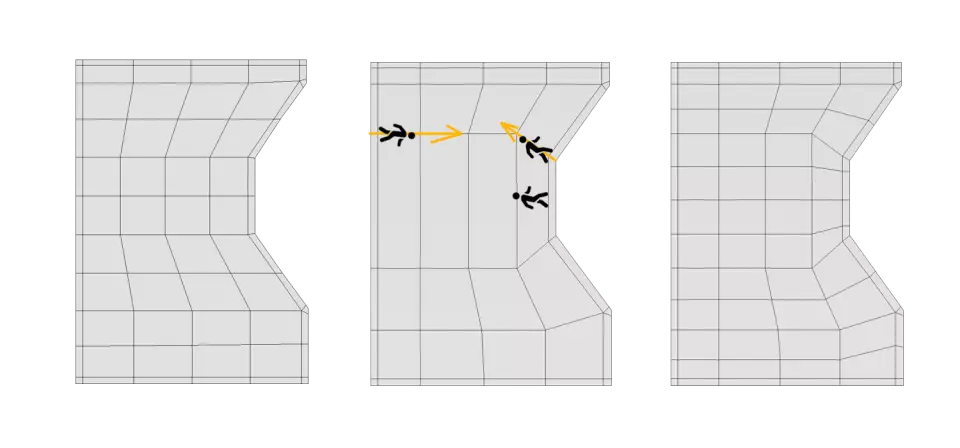
Отже, наша вихідна сітка розташована зліва. Потім, як показано в прикладі посередині, ми видалимо непотрібні нам ребра і організуємо потік тих, що не відповідають "гравітаційному" потоку. Потім, як показано в прикладі праворуч, ми повернемо ребра в середні області, щоб усі ребра знову були більш менш рівномірно розподілені.
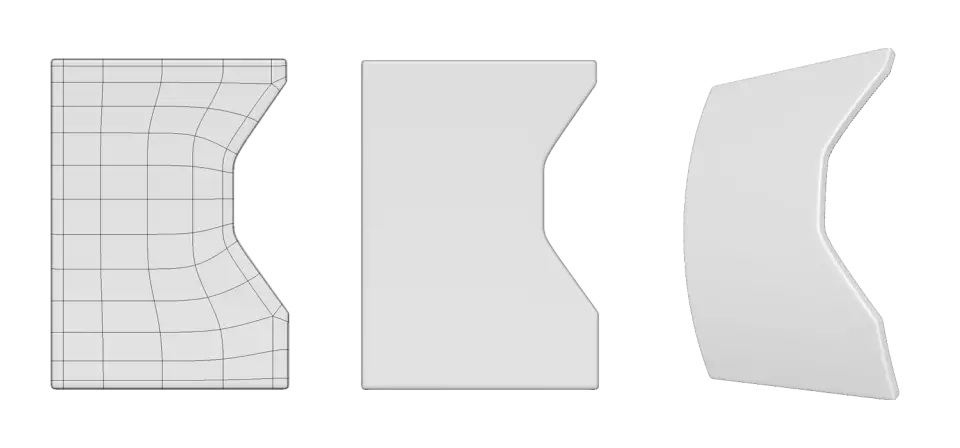
Це те, що нам потрібно! Існує безліч інших варіантів того, як ви можете це зробити, але я постарався зробити все просто та точно.
Давайте ще раз розберемо правила, якщо ми закінчили.
- Ми повинні починати з дуже низької кількості полігонів.
Чому? Тому що сіткою легше керувати і вона допомагає нам швидше створити форму.- Ми повинні переконатися, що ребра розподілені рівномірно.
Чому? Тому що ми хочемо бути впевнені, що у нас достатньо геометрії для наших деталей та гострих кутів. Нерівномірний розподіл ребер може призвести до небажаних результатів, як ми бачили в першому прикладі.- Нам потрібно додати підтримуючі ребра.
Чому? Тому що підтримуючі ребра забезпечать збереження структури нашої основної фігури (або контуру), коли ми застосуємо підрозділ.- Потрібно перевірити, чи правильно розподілені ребра.
Чому? Тому що різні потоки граней дадуть різні результати при розподілі. Ця частина вимагатиме практики.
ПРИМІТКА: Хоча ці правила можуть бути простими, деякі фактори можуть змінюватися. Наприклад, підтримуючі ребра можуть бути додані пізніше, після того, як ви впораєтеся з потоком ребер. Але це хороша практика - спочатку ознайомитися з правилами, пізніше ці ж правила можна буде легко порушувати та маніпулювати ними відповідно до вашого стилю роботи.
Перекладено з англомовного сайту, How to Understand Topology in 3D Modeling
